In the given figure, DEFG is a square and . . .

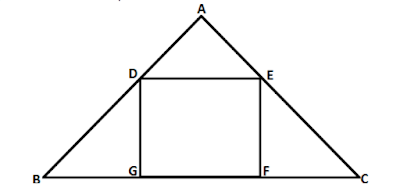
Question : In the given figure, DEFG is a square and ∠BAC = 90°. The FG² is equal to
a) BG×FC

b) BG+FC
c) BG/FC

d) None of these

Doubt by Saumya

Solution : 

∠BAC = 90° (Given)

DEFG is a square (Given)

In ΔADE and ΔGBD

∠ADE = ∠GBD (Corresponding Angles)
∠DAE=∠BGD (Each 90°)
ΔADE ~ ΔGBD (By AA Similarity) — (1)

In ΔADE and ΔFCE

∠AED = ∠FCE(Corresponding Angles)
∠EAD=∠CFE (Each 90°)
ΔADE ~ ΔFEC (By AA Similarity) — (2)

From equation (1) and (2)

ΔGBD~ΔFEC

GD/FC = GB/FE (By CPST)
GD×FE = GB×FC
FG×FG = BG×FC [∵GD=FE=FG]

FG² = BG×FC

Hence, a) would be the correct option.