21.) Show that (a-b)², (a²+b²) and (a+b)² are in AP. (2M)
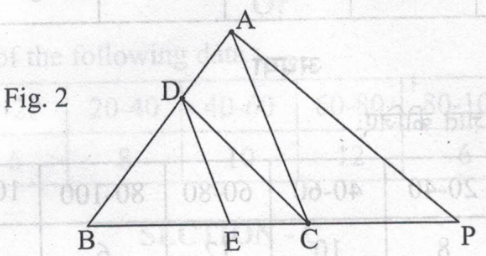
22.) In fig. 2, DE||AC and DC||AP. Prove that BE/EC = BC/CP.
OR
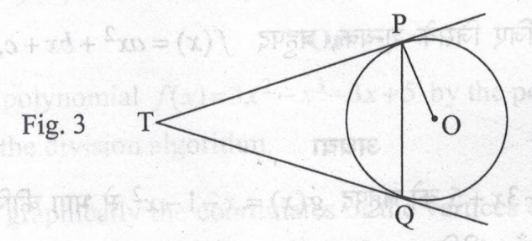
In fig. 3, two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
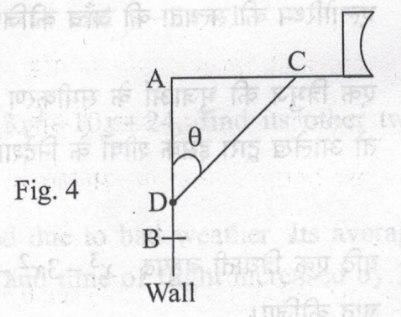
23.) The rod AC of a TV disc antenna is fixed at right angle to the wall AB and a rod CD is supporting the disc as shown in fig. 4. If AC = 1.5 m long and CD = 3 m, find (i) tanθ (ii) secθ+cosecθ.
24.) A piece of wire 22 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle. [Use π = 22/7]
25.) If a number x is chosen at random from the numbers -3, -2, -1, 0, 1, 2, 3. What is the probability that x²<=4?