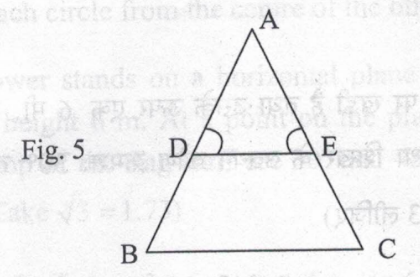
31.) In fig. 5, ∠D = ∠E and AD/DB = AE/EC, prove that BAC is an isosceles triangle.
32.) In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then prove that the angle opposite to the first side is a right angle.
33.) If sinθ + cosθ = √3, then prove that tanθ + cotθ = 1.
34.) A cone of base radius 4 cm is divided into two parts by drawing a plane through the mid point of its height and parallel to its base. Compare the volume of the two parts.
35.) Show that the square of any positive integer cannot be of the form (5q+2) or (5q+3) for any integer q. (4M)
OR
Prove that one of every three consecutive integers is divisible by 3.