Doubt by Bhavya
Solution :
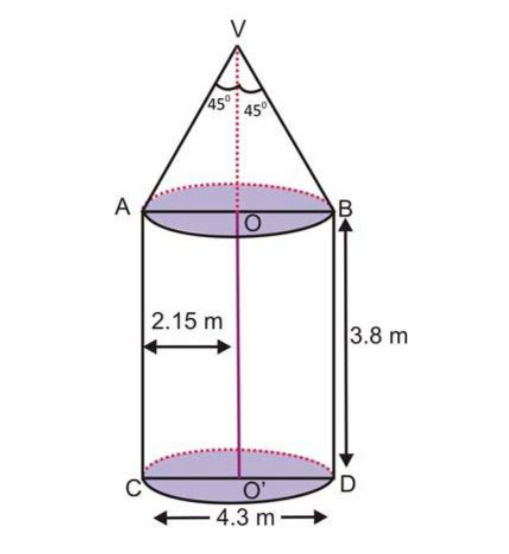
Height of Cylinder (H) = 3.8 m
Diameter of cone = Diameter of Cylinder
d = 4.3 m
r = 4.3/2
r = 2.15 m
Diameter of cone = Diameter of Cylinder
d = 4.3 m
r = 4.3/2
r = 2.15 m
Let slant height of the cone = l
and height of cone = h
Using Pythagoras Theorem
l²+l²=d²
2l²=d²
2l²=(4.3)²
2l²=18.49
l²=18.49/2
l²= 9.245
l = √9.245
l = 3.0405
l = 3.04 m
and height of cone = h
Using Pythagoras Theorem
l²+l²=d²
2l²=d²
2l²=(4.3)²
2l²=18.49
l²=18.49/2
l²= 9.245
l = √9.245
l = 3.0405
l = 3.04 m
Also, height of the cone
h = √(l²-r²)
h = √[(3.04)²-(2.15)²]
h = √[9.2416-4.6225]
h = √(l²-r²)
h = √[(3.04)²-(2.15)²]
h = √[9.2416-4.6225]
h = √4.6191
h = 2.149
h = 2.149
h = 2.15 m
Surface Area of Building
= CSA of Cone + CSA of Cylinder
= πrl + 2πrH
= πr(l+2H)
= 3.14×2.15[3.04+2(3.8)]
[Using π=3.14 because there are no factors of 7 in r, l or h]
Surface Area of Building
= CSA of Cone + CSA of Cylinder
= πrl + 2πrH
= πr(l+2H)
= 3.14×2.15[3.04+2(3.8)]
[Using π=3.14 because there are no factors of 7 in r, l or h]
= 3.14×2.15[3.04+7.6]
= 3.14×2.15[10.64]
= 6.751×10.64
=71.83064
= 71.83 m²
= 3.14×2.15[10.64]
= 6.751×10.64
=71.83064
= 71.83 m²
Now, Volume of the Building
= Volume of cone + Volume of Cylinder
= 1/3 πr²h + πr²H
= πr²(1/3h+H)
= 3.14(2.15)²[1/3(2.15)+3.8]
= 3.14(2.15)²[(2.15+11.4)/3]
= 3.14(2.15)²[(13.55)/3]
= 3.14(2.15)²[4.516]
= 3.14(2.15)²[4.52]
= 3.14×4.6225×4.52
= 3.14×4.62×4.52
= 65.570736
= 65.57 m³
= 1/3 πr²h + πr²H
= πr²(1/3h+H)
= 3.14(2.15)²[1/3(2.15)+3.8]
= 3.14(2.15)²[(2.15+11.4)/3]
= 3.14(2.15)²[(13.55)/3]
= 3.14(2.15)²[4.516]
= 3.14(2.15)²[4.52]
= 3.14×4.6225×4.52
= 3.14×4.62×4.52
= 65.570736
= 65.57 m³
Hence, surface of the building is 71.83 m² and the volume is 65.57 m³.
Note : If you want to reduce the calculation then you could also use the common sense. Try to see that VOB is an isosceles right angled triangle so radius (r) and height (h) both are equal to each other. Also slant height could be reduced to r√2.